Quick Sort

Posted on Edited on In Views:

Note about Quick Sort…

Quick sort

這篇想藉由 Leetcode 215題 複習 quick sort

TL;DR

記錄一些 quick sort 的相關筆記，盡量白話

先分享一下當初寫的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import random

class Solution:
    def find_kth(self, nums, left, right, target_idx):
        if left == right:
            return nums[left]

        pivot_val = nums[random.randint(left, right)]
        i = lt = left
        gt = right
        while i <= gt:
            if nums[i] < pivot_val:
                nums[i], nums[lt] = nums[lt], nums[i]
                lt+=1
                i+=1
            elif nums[i] == pivot_val:
                i+=1
            elif nums[i] > pivot_val:
                nums[i], nums[gt] = nums[gt], nums[i]
                gt-=1

        if lt <= target_idx <= gt:
            return nums[lt]
        elif target_idx < lt:
            right = lt-1
            return self.find_kth(nums, left, right, target_idx)
        elif target_idx > gt:
            left = gt+1
            return self.find_kth(nums, left, right, target_idx)

    def findKthLargest(self, nums: List[int], k: int) -> int:
        left, right = 0, len(nums)-1
        target_idx = len(nums)-k
        return self.find_kth(nums, left, right, target_idx)

What is Quick Sort?

Quick Sort 的核心步驟是：

  1. 選取陣列中的一個數字當作 pivot 值（可以是任意位置，常見的選擇有：最右邊、最左邊、中間或隨機位置）
  2. 分割過程：
  • 從左到右遍歷陣列，將小於 pivot 的數字放到左邊
  • 將大於 pivot 的數字放到右邊
  • 最終 pivot 會被放在其正確的位置
  1. 對左右兩個子陣列重複執行上述步驟，直到子陣列的長度小於等於 1
  2. 這個過程通過遞迴的方式，逐步將大問題分解成小問題來解決，最終完成整個陣列的排序。
  3. 整體時間複雜度 : O(NlogN) ; 空間複雜度 : O(1)

為什麼時間複雜度是 O(NlogN) ？

  • 概念上每次跟 pivot 值比較完都會把 list 一分為二，假設總共有 N 個元素，每除以一次 2 就會多一層, 最後除到結果為 1 停止，簡單來說，除了幾次就有幾層。

    1
    2
    3
    4
    5
    6
    7
    N*(1/2)*(1/2)*.... = 1

    N*(1/2)^k = 1

    N = 2^k

    k = logN

    所以層數為 logN 層

  • 那每一層要做的事就是跟 pivot 值比較，假設我們有一個長度為 N 的 list，每次都能完美地均分（理想情況）：

    1. 第1層：N-1 次比較
    • 例如 N=8 時，需要比較 7 次（不算 pivot）
    1. 第2層：兩個子數組，每個長度約 N/2
    • 左半：(N/2)-1 次比較 (不算 pivot）
    • 右半：(N/2)-1 次比較 (不算 pivot）
    • 總共：N-2 次比較
    1. 第3層：四個子數組，每個長度約 N/4
    • 每個子數組需要 (N/4)-1 次比較
    • 總共：N-4 次比較

    所以總比較次數會是

    1
    (N-1) + (N-2) + (N-4) + ... + (N-C)

    在分析時間複雜度時，可以忽略這些常數項（-1, -2, -4…）

    1
    2
    3
    T(N) = (N-1) + (N-2) + (N-4) + ... + (N-C)
    ≤ N + N + N + ... + N （logN 次）
    = N * logN

  • 所以時間複雜度為 O(NlogN)

worst case 會變 O(N^2)

  • 上述最好的情況是，pivot 值挑的好，如果 pivot 剛好是最大或最小，不會產生 divide & conquer 的效果 ，層數也不會是 logN，會變成 N 層。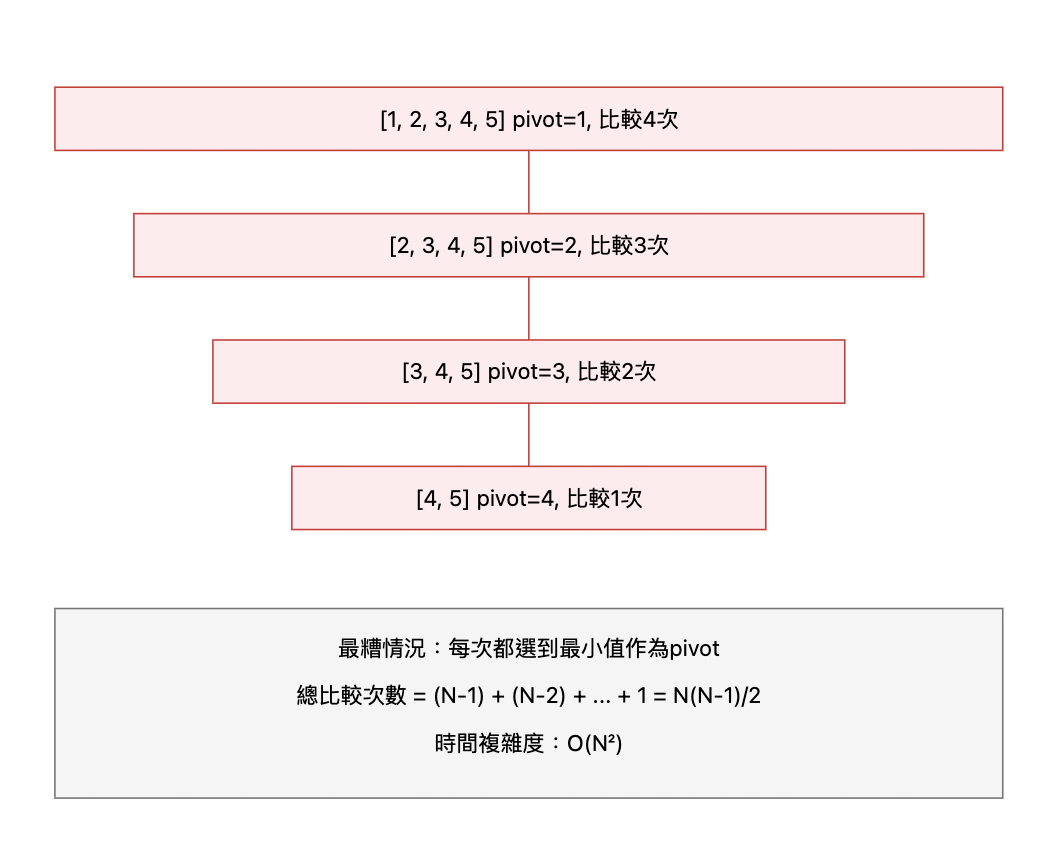

  • 重點是挑出來的那個 pivot value 能夠盡量把 list 平分。

如果 list 中有重複數字？

另一種情況需注意的是，如果 list 內有很多重複的數字, 假設用原先的方式去 divide 會有問題, 一樣會造成O(N^2)，假設原先的區分方式是 ≤ pivot value 的放到左邊, > pivot value 放到右邊，以較極端的 list 裡全部都是重複數字, 造成一直選到重複數字當 pivot value, 變成每次 divide 後產生嚴重不平衡的 tree，和上面的 worst case 一樣。

divide 的方式需優化 : three way partition

list 不再分成兩部分, 分成三部分 <pivot , =pivot , >pivot。

  • two way divide

    1. 假設每次都取最後一個元素當成 pivot value

    2. in place 分割之後, pivot value 的位置可能會變

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    # [100, 2, 44, 4, 5, 35] => pivot value 35

    # after divide => [2, 4, 5, 35, 44, 100]

    >>> def divide(nums):
    ...     pivot_value = nums[-1]
    ...     tracking_idx = 0
    ...     for i in range(len(nums)-1):
    ...         if nums[i] < pivot_value:
    ...             nums[i], nums[tracking_idx] = nums[tracking_idx], nums[i]
    ...             tracking_idx+=1
    ...     nums[-1], nums[tracking_idx] = nums[tracking_idx], nums[-1]
    ...     print(nums)
    ...
    >>> divide([100,2,44,4,5,35])
    ...
    [2, 4, 5, 35, 44, 100]

  • three way divide

    1. 一樣假設每次都取最後一個元素當成 pivot value

    2. in place 分割之後, 會分成三個部分

    3. 不用 tracking_idx

    4. 概念上要追蹤重複元素區間的最左邊idx和最右邊的idx ⇒ lt & gt

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    nums = [2, 1, 2, 2, 4, 2, 1, 2]

    取最後一個元素2當作 pivot value
    初始化 lt = i = 0 ; gt = len(nums)-1
    # 第一個元素 (2)：等於pivot, lt 不變, i+=1
    [2, 1, 2, 2, 4, 2, 1, 2]
    i                    gt
    lt

    # 第二個元素 (1)：小於pivot, lt和i互換, lt+=1 i+=1
    [2, 1, 2, 2, 4, 2, 1, 2]
        i                 gt
    lt

    # 第三個元素 (2)：等於pivot, lt 不變, i+=1
    [1, 2, 2, 2, 4, 2, 1, 2]
        i              gt
    lt

    # 第四個元素 (2)：等於pivot, lt 不變, i+=1
    [1, 2, 2, 2, 4, 2, 1, 2]
            i           gt
    lt

    # 第五個元素 (4)：大於pivot, gt和i互換, gt-=1, i不+1, 因為剛換過來的值還沒比較過
    [1, 2, 2, 2, 4, 2, 1, 2]
                i        gt
    lt

    # 第五個元素 (2)：等於pivot, lt 不變, i+=1
    [1, 2, 2, 2, 2, 2, 1, 4]
                i     gt
    lt

    # 第六個元素 (2)：等於pivot, lt 不變, i+=1
    [1, 2, 2, 2, 2, 2, 1, 4]
                    i  gt
    lt

    # 第七個元素 (1)：小於pivot, lt和i互換, lt+=1 i+=1
    [1, 2, 2, 2, 2, 2, 1, 4]
                    i
                    gt
    lt

    # 此時i已經超過gt, 停止比較
    [1, 1, 2, 2, 2, 2, 2, 4]
                        i
                    gt
        lt

    # 最終結果
    [1, 1 | 2, 2, 2, 2, 2 | 4]
            lt          gt
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    >>> def three_way_divide(nums):
    ...     pivot_value = nums[-1]
    ...     lt = i = 0
    ...     gt = len(nums)-1
    ...     while i<=gt:
    ...         if nums[i] < pivot_value:
    ...             nums[i], nums[lt] = nums[lt], nums[i]
    ...             lt+=1
    ...             i+=1
    ...         elif nums[i] == pivot_value:
    ...             i+=1
    ...         elif nums[i] > pivot_value:
    ...             nums[i], nums[gt] = nums[gt], nums[i]
    ...             gt-=1
    ...     print(nums)
    ...
    >>> three_way_divide([2, 1, 2, 2, 4, 2, 1, 2])
    [1, 1, 2, 2, 2, 2, 2, 4]

Quick Select

Leetcode 215 題應用由 quick sort 延伸的 quick select，其中的分割方式為 three way partition。

  • quick select 時間複雜度 ⇒ O(N)

  • 假設有一個長度為 N 的數列，每次都能完美地均分（最理想情況）：

    1. 第1層：N-1 次比較
    • 例如 N=8 時，需要比較 7 次（不算 pivot）
    1. 第2層：兩個子數列，每個長度約 N/2 ，此時只需處理某一邊
    • (N/2)-1 次比較 （不算 pivot）
    1. 第3層：四個子數列，每個長度約 N/4，此時只需處理某一邊
    • (N/4)-1 次比較 （不算 pivot）

總比較次數會是

1
2
3
4
5
6
7
8
9
(N-1) + (N/2-1) + (N/4-1) + ... + 1

#忽略-1部分
N + 2/N + N/4 + ... + 1 #共 logN層

#等比級數公式
total = a(1-r^n)/(1-r) = N(1-(1/2)^logN) / (1/2)
= N(1-1/N)/(1/2)
= 2N-2

分析時間複雜度時，得到 O(N)

👋👋👋